J.R. once told me about a friend who wrote a computer program that found the shape of a hanging spring. The shape of a hanging chain is a "catenary" [i.e. y=cosh(x)], a fact I was aware of but didn't know how to prove. The shape of the hanging spring (specifically, a spring with zero rest length but finite mass, and whose density is therefore a delta function) turns out to be a parabola.
The program apparently discovered this by starting with a string of many springs of zero mass and zero rest length connecting point particles with mass. The point particles start off stretching in a straight line between two supports of the same height, horizontally separated by some fixed distance. So it's like the spring hanging from the towers that support a suspension bridge. The difference is there's no bridge, and the spring is stretchy whereas the cables on the bridge basically are not.
The program then calculated the forces from gravity and the springs, took a small step forward in time using F=ma, recalculated the forces, took another step, etc. until the thing came to rest. There must have been a small damping coefficient in the program as well to keep the spring from oscillating forever.
I wanted to solve this problem analytically, but at the time I didn't know how. Later, I saw the solution to the catenary problem in a discussion of the calculus of variations. In this approach, you write a function for the energy of the chain/spring, then use a variational principle to minimize the energy.
However, I today I read about how to treat a similar problem, where you have a massless, nonstretchy chain supporting a massive, flat road (i.e. suspension bridge). Modifying the book's solution a bit, I found that you can solve all three problems (massive chain, massive spring, massless chain with bridge) using only single-variable calculus. Here is how:
Assume the spring has some shape given by the function height = y = f(x), where x is the distance from the middle of the two supports.
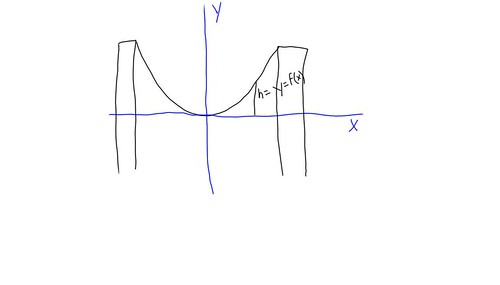
Our plan will be to find a differential equation for y using the following assumptions:
- The system is in equilibrium
- The tension in the spring/chain at a point must be along the direction of the tangent to that point.
- The only external force on the spring is gravity, which is in the y-direction.
Not only must the entire spring be in equilibrium, but every differential element ds of the spring must be in equilibrium. So consider the forces acting on an element of the spring ds, as shown below:
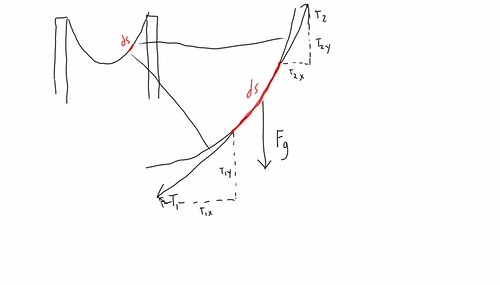
The condition of equilibrium in the x-direction requires
T
1x - T
2x = 0
T
1x = T
2x = T
0.
In the y-direction, equilibrium requires
-T
1y + T
2y - F
g = 0
rewriting F
g as p
x(x)*g*dx, where p
x(x) is the mass density per unit distance in the x-direction at the point x (NOT necessarily the same as the mass density of the spring, p
s), this becomes
-T
1y + T
2y = p
x(x)*g*dx
Now we invoke the fact that the tension is along the spring.
T
y/T
x = y'
but we found earlier that T
x = T
0, so
T
y = T
0*y'
so going back to the eqn for equilibrium in the y-direction:
T
0*[y'(x
2) - y'(x
1)] = p
x(x)*g*dx
for sufficiently small segment ds, this becomes
T
0*y''(x)*dx = p
x(x)*g*dx
y''(x) = p
x(x)*(g/T
0)
Now we have the desired differential equation in y. So far, the solution to all three problems is the same. Now they diverge, because the mass density is different in the three cases.
Massless Chain Supporting a Road:
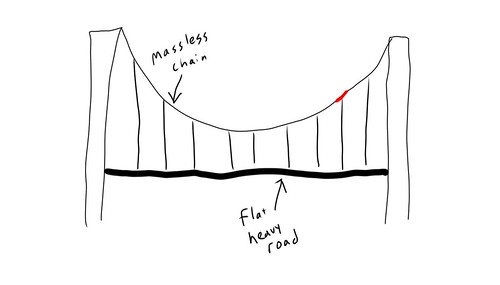
Here, the mass density is just the mass of the road per unit in the x-direction
p
x = p
0y''(x) = p
0*g/T
0 = C
where C is some constant. Integrating, we get a quadratic - the massless chain supporting a road hangs in the shape of a parabola.
This could potentially be a useful result, because people are interesting in making parabolas, because a parabola is the ideal shape for telescopes, radio antennas, etc.
Massive chain:

The mass density of the chain is constant:
p
s = p
0From the geometry of the situation, we can get p
x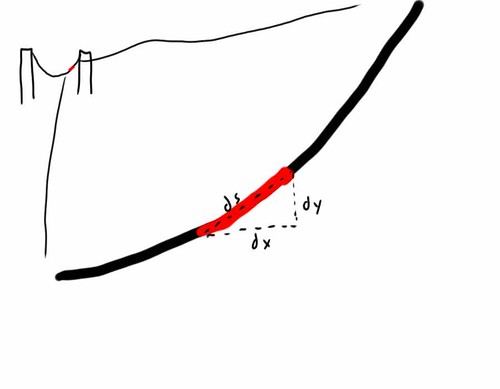
ds
2 = dx
2 + dy
2ds/dx = (1 + y'
2)
1/2*dx
p
x*dx = p
s*ds
p
x = (1 + y'(x)
2)
1/2*p
0substituting into the D.E.
y'' = (1 + y'
2)
1/2 * C
where I mashed the constant together
make a substitution z=y', z'=y''
dz/dx = (1 + z
2)
1/2*C
dz/(1 + z
2)
1/2 = C*dx
Look this integral up and you get sinh
-1(z) = C*x
z = sinh(C*x) = y'
y = cosh(c*x), which is the shape of a catenary
Massive Spring
For the massive spring, we have to take a look at Hooke's Law:
T = k*x, where x is the displacement from equilibrium.
Note that if we stretch a string to a length x, its density becomes m/x, where m is the length of the spring.
p
s(x) = 1/T(x)
where T is the tension and I suppressed a constant.
T = (T
x2 + T
y2)
1/2T = [T
02 + (T
0y')
2]
1/2using earlier results for T
x and T
yT = T
0*(1 + y'
2)
1/2p
s = 1/T = 1/(1 + y'
2)
1/2p
x = (1 + y'
2)
1/2*p
s, as in the previous case
p
x = [(1 + y'
2)
1/2]/[(1 + y'
2)
1/2]
p
x = 1
again suppressing constants.
So this case is the same as the original problem with the road hanging from a chain, and the hanging spring of zero rest length takes the shape of a parabola.
Additionally, by modifying the function p
x, you could find the differential equation for the shape of the bridge under an arbitrary load, such as combining all three methods to model a suspension bridge supporting a road where the cables have some finite mass and also some Young's modulus, and finite rest length. You could add traffic going across, acceleration of the road when lifting it up to allow a boat to go underneath, etc. Note that a point mass traveling across the bridge hanging from a chain would cause the density function to become a delta function at that point. So y'' is a delta function, y' has a discrete jump, and the result is that a heavy truck driving across such a bridge causes a kink in the cable directly above the truck.








